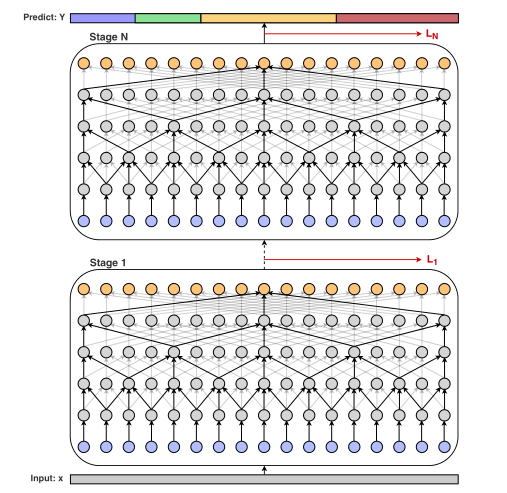
6_2图像卷积疑问及解答
问题1:卷积是什么?
解答1:小明吃饭
举例说明,有个小明一天到晚在吃东西,时间和他吃下去的东西的函数图像如下图所示:
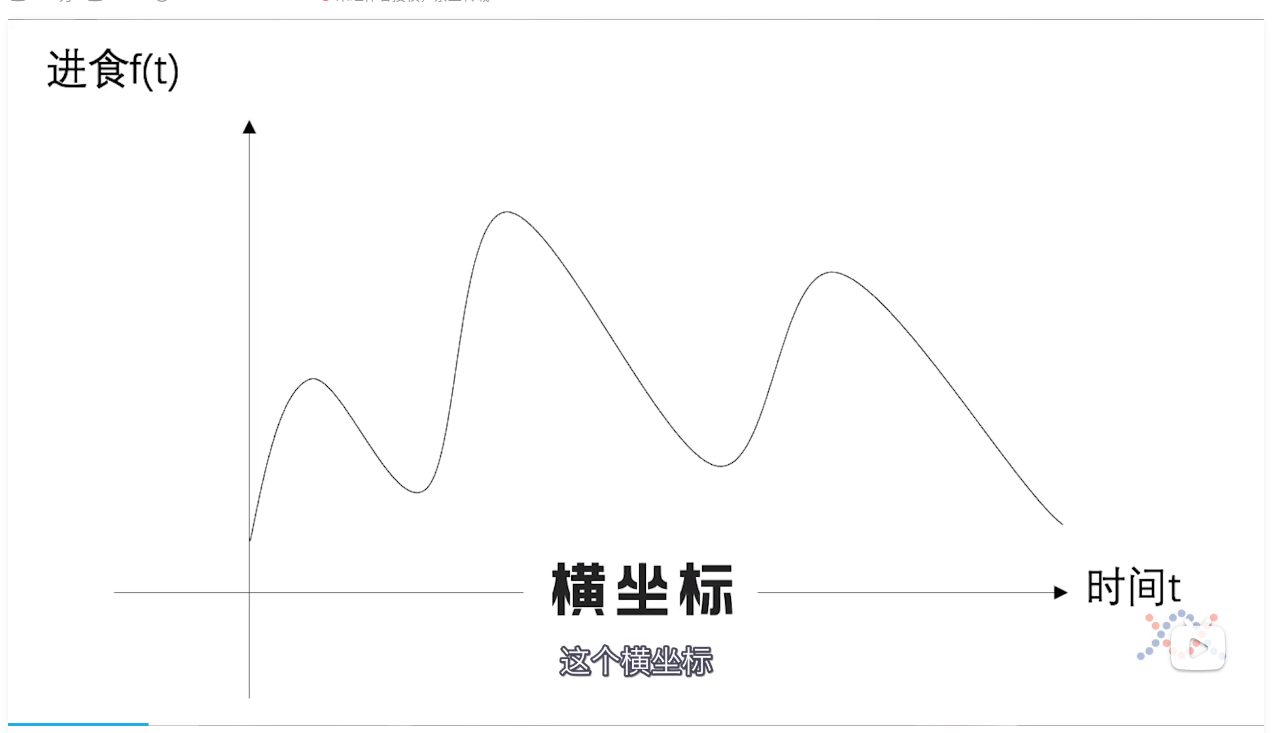
他消化的速率如下图所示:
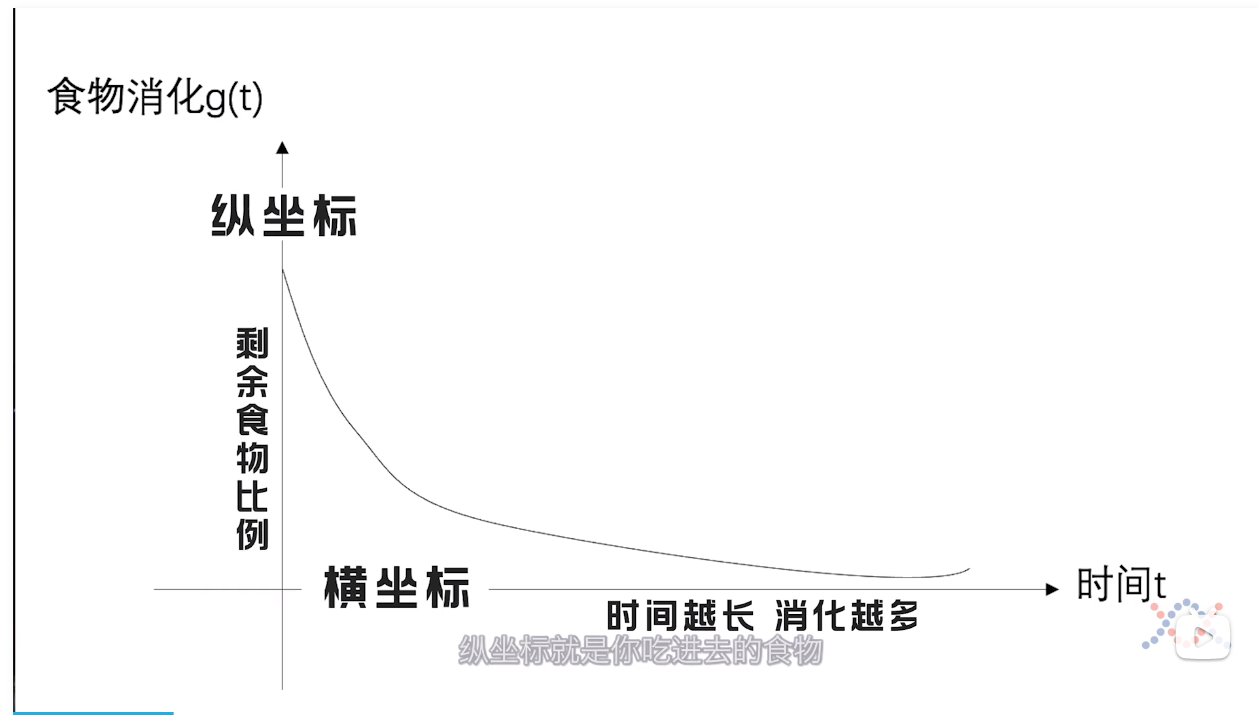
卷积的公式为:
用f函数表示进食,g函数表示消化,带入到卷积公式之中.注意,g函数表示的是消化后剩余食物所占的比例.
这里要表现的东西其实用一根线将f函数和g函数联系了起来.
一个系统输入不稳定(对应f函数),但是输出稳定(对应g函数),可以用卷积来求系统存量.
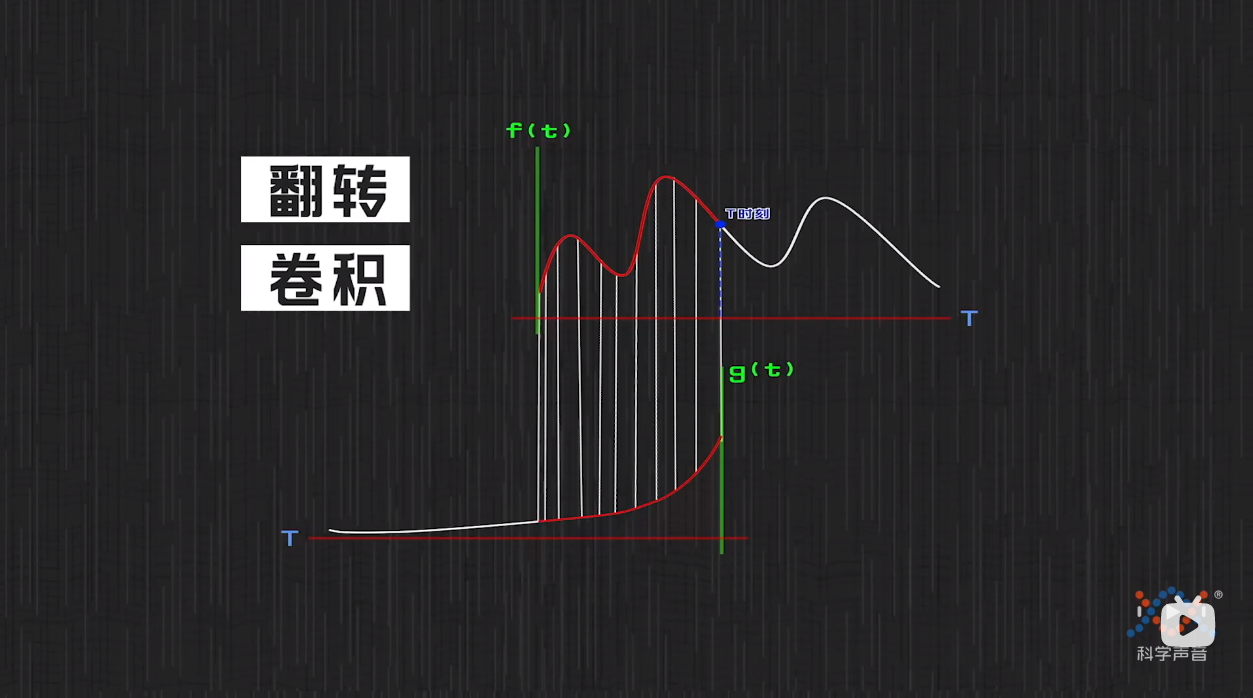
讲其对应到可视化图像上,其实就是讲g函数翻转了一下和f函数对应相乘,因为翻转了,所以对应叫做卷积.
问题2:如何将卷积公式与计算机图像处理对应起来
解答2:
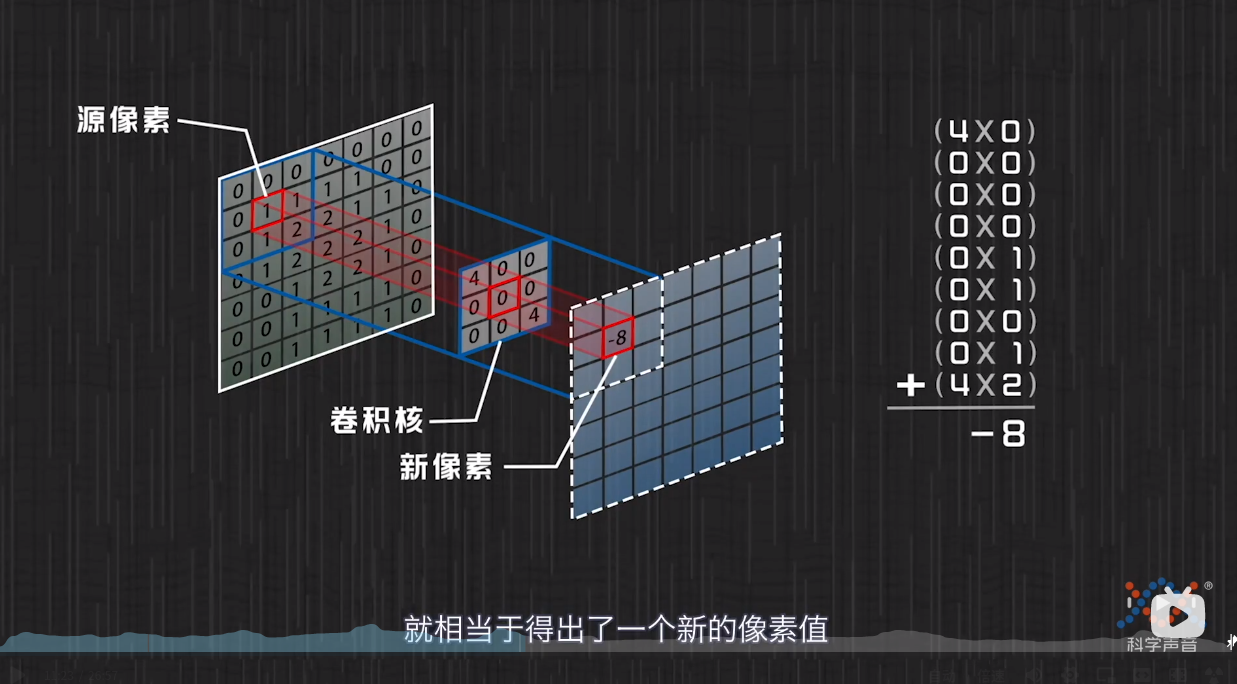
上图为计算机对图片进行卷积处理的解释,和前面的卷积公式有一对应结构:先相乘再相加,然后得到一个新的像素值.
但是这么做会导致图像少一圈像素,那么就在原图像的外围加一圈0的像素点,如下图所示:这样就能得到同样大小的图片
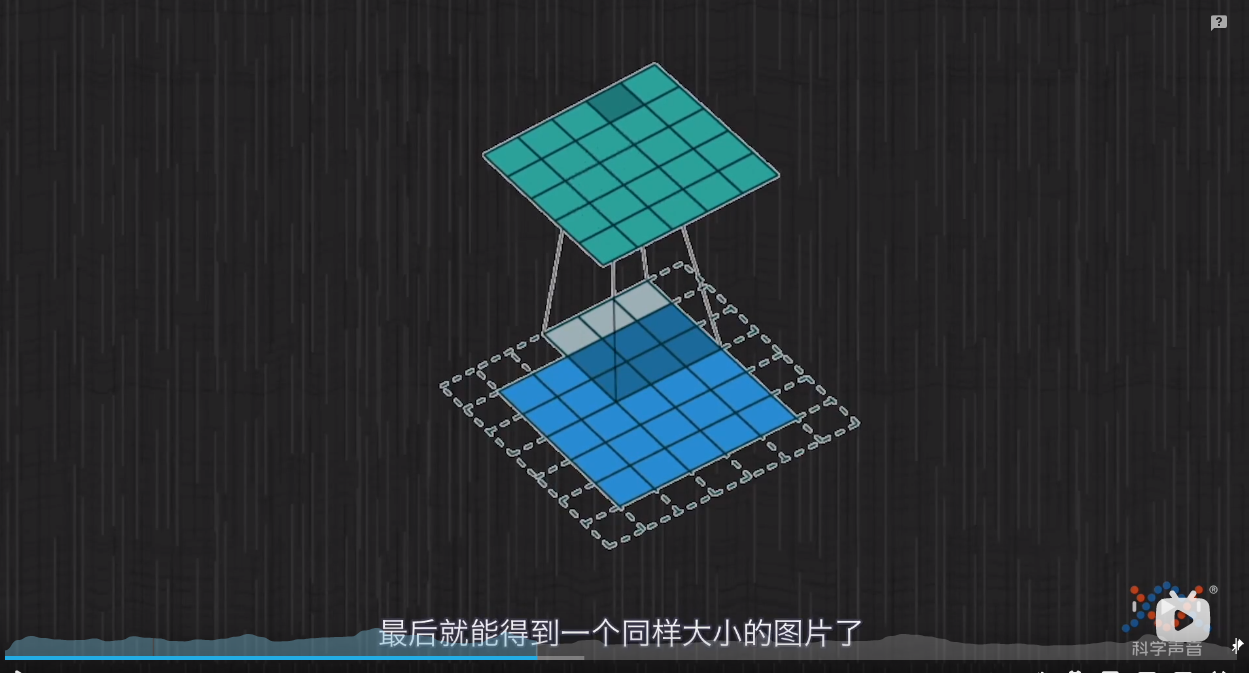
图像对应卷积公式中的f函数,卷积核对应g函数,这里与吃东西不同之处在于这里是一个二维的问题.
问题3:如何理解卷积本质?
解答3:
在一个时间段上,会随机的发生很多件事情,这些事情是无法预测的随机的输出,同时每一件事情都可能会对后面的事情产生一定的影响,这个影响会随着时间的变化而变化,其函数对应g函数.注意,这里的g函数可以随意变化,横坐标不一定时间,函数图线不一定是递减,
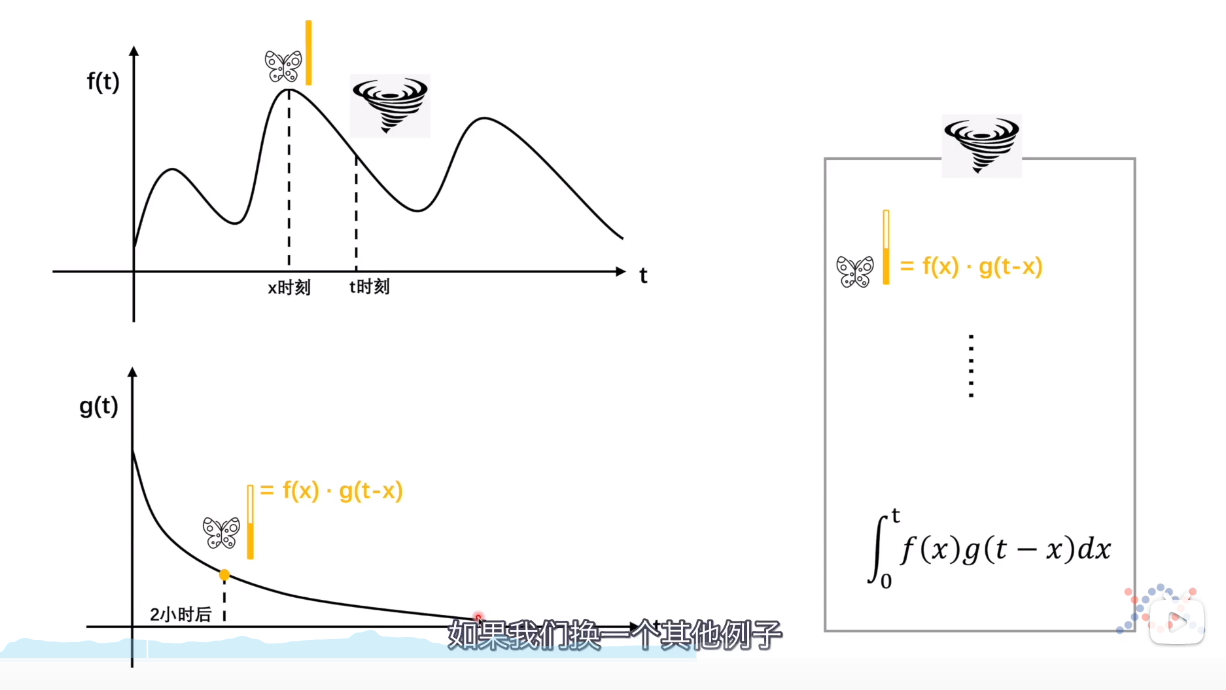
举例说明:在某一个时刻,发生了一件事,这件事会受到之前发生的很多事情的影响,这个影响还会随着时间的改变而改变,这个改变的规律的函数就是g函数.
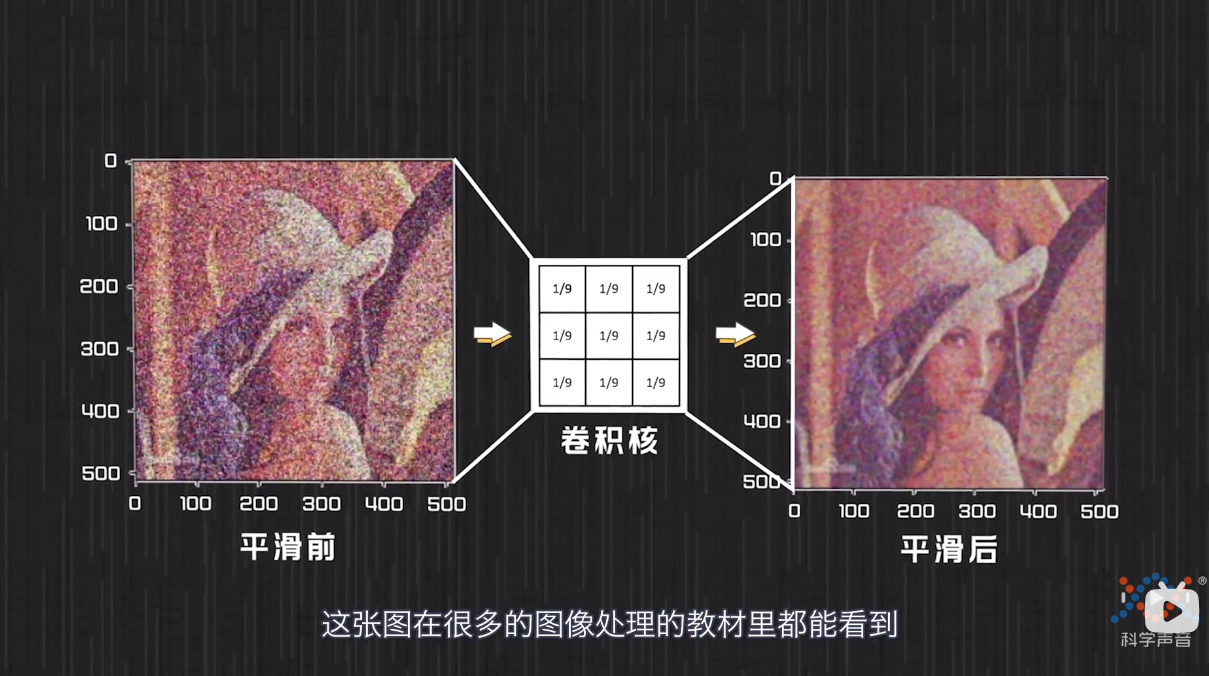
这里g函数所做的操作就是求了一个平均,这里g函数是一个3 3的卷积核,就是表达的是一个像素点周围的一圈像素点对其产生的影响.还会有5 5等多种大小规模的卷积核.
卷积核的规模大小对应的是能够影响中心点的周边的点的范围,卷积核每一个小格里的函数对应的是周边点对中心点影响的g函数.



注意,这里需要将相应的矩阵进行180°翻转才能转化成一一对应的关系.
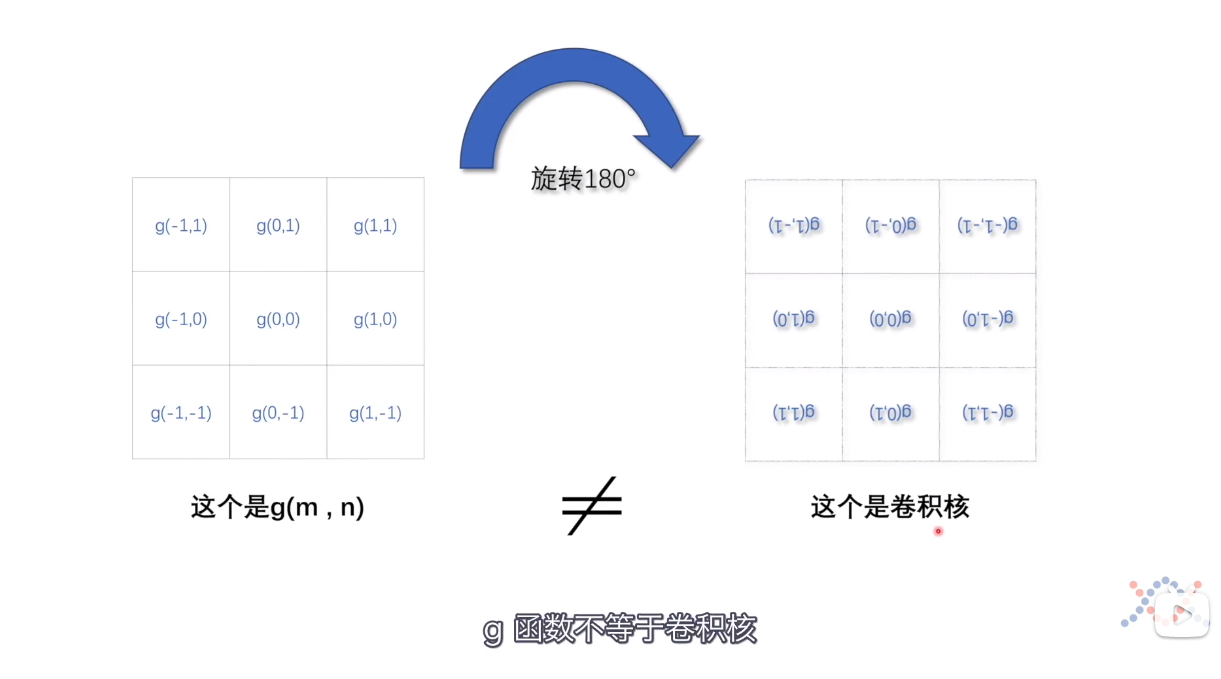
这就说明g函数不等于卷积核,需要讲g函数的矩阵顺时针翻转180°才是卷积核.卷积核可以直接扣在图像上进行相乘再相加.
- 过去对现在的影响就相当于周围像素点对中间像素点的影响;
- g函数规定了如何影响;
问题4:卷积神经网络
卷积神经网络第一步:将图像的局部特征提取出来,讲这些局部特征交给神经网络.
如何提取局部特征?就是对图像进行卷积操作.这里与之前理解的卷积的操作的结果有不同之处,该如何理解?
解答4:
因为卷积核有很多种,不止有平滑卷积核.

上面的两个卷积核,第一个卷积核讲垂直方向的边界挑选了出来(垂直边界过滤器),下面的将水平方向的边界挑选了出来(水平边界过滤器).
也就是说,只要卷积核应用合理,就能将图片中特定的特征提取出来,别的东西过滤掉.

上图所示三个卷积核分别就是提取三个唯独的特征信息.
总结:
- 不稳定输入,稳定输出,求系统存量;
- 周围像素点如何对中心像素点产生影响;
- 作为过滤器,提取图片特征信息.,也就是指中心像素点如何试探周围的像素点,如何筛选图像特征.