MS-TCN：用于动作分割的多阶段时间卷积网络

摘要

传统方法：首先生成逐帧概率，然后再将其送到高级时间模型

最近方法：采用时间卷积直接对视频的每一帧进行分类

本文：提出了一种用于时间动作分割任务的多阶段架构，每个阶段都具有一组扩张时间卷积，用来生成由下一个阶段细化的初始预测。损失函数包含分类损失和平滑损失，平滑损失能够对过度分割的情况进行惩罚。

实验数据集包括：50Salads、Georgia Tech Egocentric Activities (GTEA)、the Breakfast dataset

简介

早期动作分割方法包括滑动窗口方法和马尔可夫模型，但是它们的检测速度非常慢。

随着语音模型的发展，依靠时间卷积来捕获视频帧之间的远程依赖关系的方法受到关注，但是这些方法依旧存在检测速度慢、一秒只有几帧的缺陷。

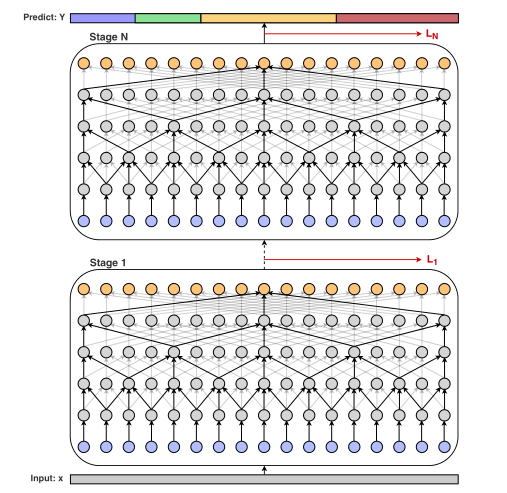
该文章提出了一种多阶段时间卷积网络，通过对视频的全时间分辨率进行操作从而获得更好的检测结果。

该模型每一个阶段的输出都是下一个阶段的输入。在每一个阶段中都使用一系列的一维空洞卷积，使得模型能引入更少的参数而获得更大的时间感受野。同时，采用平滑损失来惩罚过度分割的错误。

本文贡献：1.提出了多阶段时间卷积架构；2.引入平滑损失函数来提高预测质量。

时间动作分割

给定视频$x{1:T}=(x_1,…,x_T)$，目标是推断每一帧的类别标签$c{1:T}=(c_1,…,c_T)$，其中，$T$为视频的帧数.

单阶段TCN

单阶段模型仅包含时间卷积层.不采用池化层来减低时间分辨率(视频帧数),也不采用全连接层;挨强势将输入的大小修改为固定大小.

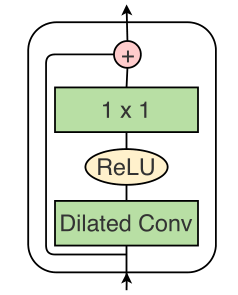
第一层为$1\times1$卷积层,用来调整输入的特征维度和模型中的维度相匹配.然后,在这一层之后是一层一维膨胀卷积层,膨胀因子以此为1,2,4,…,512.所有层都有相同数量的卷积滤波器(有相同数量的输出通道),其卷积核大小为3.每一层都有ReLU进行激活.同时,进一步采用残差连接来促进梯度流.

$\hat{H_l}=ReLU(W_1*H_{l-1}+b_1)\tag{1}$ $H_l=H_{l-1}+W_2*\hat{H_l}+b_2\tag{2}$

其中,$H_l$是第$l$层的输出,$*$表示卷积操作,$W_1 \in R^{3 \times D \times D}$是卷积核大小为3 的膨胀卷积滤波器的权重,$W_2 \in R^{1 \times D \times D}$是$1\times1$卷积层的权重,$D$是卷积滤波器的数量,$b_1,b_2 \in R^D$是偏置向量.其具体操作如下图所示.

使用膨胀卷积可以在不增加模型参数量的情况下增加模型的感受野,每一层的感受野大小公式如下:

$ReceptiveField(l)=2^{l+1}-1 \tag{3}$

其中,$l \in [1,L]$是层数,注意该公式只适用于大小为3的卷积核.为了获得分类结果,在最后一个膨胀卷积层的输出上采用$1\times1$卷积,并用softmax激活.,如下公式所示:

$Y_t=Softmax(Wh_{L,t}+b) \tag{4}$

其中,$Yt$表示在第$t$帧的分类标签,$h{L,t}$是最后一个膨胀卷积层在第$t$帧的输出,$W \in R^{C \times D}$和$b \in R^C$是$1\times1$卷积的权重和偏置,$C$是类别数量,$D$是卷积滤波器的数量.

多阶段TCN

在多阶段模型中,每个阶段从前一阶段获取初始预测并对其进行细化,具体公式如下:

$Y^0=x_{1:T} \tag{5}$ $Y^s=\mathcal{F}(Y^{s-1}) \tag{6}$

其中,$Y^s$表示第$s$阶段的输出,$\mathcal{F}$表示之前提到的单阶段TCN.只用这种多阶段架构有助于提供更多上下文来预测每一帧的类标签.

损失函数

采用分类损失和平滑损失的组合.

在分类损失中,采用交叉熵损失,公式如下:

$\mathcal{L}_{cls} = \frac{1}{T} \sum_t - \log(y_{t,c}) \tag{7}$

其中,$y_{t,c}$表示第$t$帧的对应类别的预测标签.

尽管交叉熵损失已经表现良好,但是在预测结果中包含一些分割过度的问题.为了进一步提高预测质量,使用额外的平滑损失来减少这种分割过度的问题.对于这种损失,在逐帧概率上使用截断均方误差:

$\mathcal{L}_{T-MSE} = \frac{1}{TC} \sum_{t,c} \hat{\Delta}_{t,c}^2 \tag{8}$ $\hat{\Delta}_{t,c}= \left \{ \begin{array}{lr} \Delta_{t,c} & : \Delta_{t,c} \leq 0\\ \mathcal{T} & : otherwise \end{array} \right. \tag{8}$ $\Delta_{t,c} = |\log{y_{t,c}} - \log{y_{t-1,c}}| \tag{10}$

其中,$T$是视频长度(帧数),$C$是目标类别数量,$y_{t,c}$是第$c$类在第$t$帧的概率.

注意,梯度仅根据$y{t,c}$计算,而不是$y{t-1,c}$.

最终的损失函数如下所示:

$\mathcal{L}_s = \mathcal{L}_{cls} + \lambda \mathcal{L}_{T-MSE} \tag{11}$

其中,$\lambda$是一个模型超参数,用来控制每种损失函数的具体贡献.最后为了训练完整模型,最小化所有阶段的损失总和:

$\mathcal{L} = \sum_s{ \mathcal{L_s} } \tag{12}$

模型整体采用了四个阶段的多阶段架构,每个阶段包含十个膨胀卷积层,其中每一层的膨胀因子都加倍,并在每一层之后使用dropout.将模型所有层的滤波器数量设置为64,滤波器大小为3(输出通道数为64,卷积核大小为3,注意这里为一维卷积核).对于损失函数,$t=4$,$\lambda=0.15$,同时使用学习率为0.0005的Adam优化器.

实验

数据集采用了50Salads,GTEA,Breakfast.对于所有数据集,提取视频中的I3D特征,并将这些特征用作模型的输入.

MS-TCN:Multi-Stage Temporal Convolutional Network for Action Segmentation